
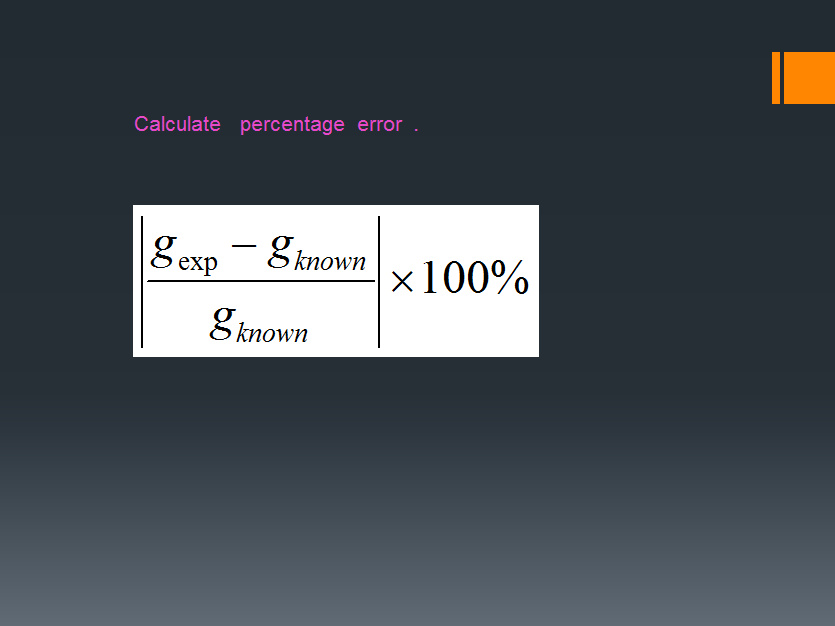
Draw a pencil line across the width of the card at exactly half its length. Clamp a ruler so that the vertical distance may be measured from above the level of the light gate.Ĭut black card to the precise length of 10.0 cm. Read our standard health & safety guidanceĬlamp the light gate about 20 cm above the bench. The emphasis of this datalogging experiment is on investigating the relationship between the velocity of the card and the distance it has fallen from rest. The acceleration of an object allowed to fall under the force of gravity is found by dropping a card vertically through a light gate. However, this affected both string and accuracy of the data due to unknown stretch. Calculation of maximum centripetal acceleration commenced with the aid of angle created by pendulum (where PE converted to KE).
To rectify this problem in the next experiment, it would be essential to use a light string as well as measuring stretch before starting. It entailed one hour to wait for effective completion of string’s stretch and twist caused by the suspended mass, which was a lot of time. There was also a need to increase the length of the string to ensure less percentage error restricted by 8m measuring tape (stairs were approximately 15m high).Īccuracy’s margin was set at ±5 or approximately 0.07% over 7.5m. Then calculating mass of the string compared to that of the sinker commenced. The purpose of the latter was to ensure the center of pendulum’s oscillation system was as close as possible to the center of the mass of fishing sinker. This is because 1.10 x 1.10 = 1.21 Controlling and measuring length String used in this experiment was light together with heavy mass. Suppose T had an error bearing a margin of 10%, this will reflect 21% value of g. In addition, an error in g exhibited a squared or parabolic relationship with error evident in the value of T. This implies suppose there was a 10% error in value of l, it will reflect an erratic value of g having a margin of 10%. Results Table 1: Data Results L (M) T50 (S) T (S) T (S) T (S) T (S) T2 (S2) g (M/S2) 50 65 80 95 110 Discussion Formula and effects on experimental accuracy Based on the experimental results, error in L prompts a linear relation error in any resulting value of g. T2 graph with the intention of ascertaining its slope, which was the value for g (Serway, Jewett & Vahe? 465). The last step encompassed plotting of L vs.

Recording of data included g and its mean values besides standard error deviations. After tabulation, calculation commenced to ascertain T2 and g values. Timing was at intervals of 10 oscillations for each chosen L until it reached about 125cm and having at intervals of 15cm, then tabulating obtained data.
It was essential to ensure motion in this case was vertical instead of erratic elliptical, which mostly develops due to inappropriate displacement. Then displacement of a pendulum using a certain angle before released to swing back and forth took place. This is by hanging pendulum or bob using a string from the supporting board where there is a hook, then adjusting L to approximately 50cm or appropriate length that will act as the initial value. L / T2 Methodology Experiment Materials required Piece of string, which is lighter such that its weight is negligible Hook Pendulum or bob Stopwatch Meter rule or tape measure Supporting board for hook Steps to perform experiment The first step entailed setting up the experiment. In quest to find g, this experiment utilizes the following formula, T = 2? / ? = 2? v (L/g) = 2? v (L/g) by rearranging g = 2? This is because at the poles the surface is flattened compared to the equator where there is bulging due to a large radius, which is the reason behind an individual’s location being the determinant of g. This is due to earth’s radii changes caused by both altitude and latitude variations as one moves to the poles whereby distance to the crust continues to decrease.


 0 kommentar(er)
0 kommentar(er)
